Heptagonalinės prizmės savybės ir kaip apskaičiuoti tūrį
A heptaginė prizmė yra geometrinis paveikslas, kuris, kaip rodo pavadinimas, apima dvi geometrines apibrėžtis: prizmę ir heptagoną.
„Prizma“ - tai geometrinis paveikslas, kurį riboja dvi bazės, kurios yra lygios ir lygiagrečios daugiakampiai, o jų šoniniai veidai yra lygiagretės.
„Heptagonas“ yra daugiakampis, kurį sudaro septynios (7) pusės. Kadangi heptagonas yra daugiakampis, gali būti, kad jis yra reguliarus arba nereguliarus.
Manoma, kad daugiakampis yra reguliarus, jei visos jo pusės turi tokį patį ilgį ir jų vidiniai kampai yra tokie patys, jie taip pat vadinami lygiaverčiais daugiakampiais; kitaip sakoma, kad daugiakampis yra nereguliarus.

Heptagoninės prizmės savybės
Toliau pateikiami tam tikri bruožai, turintys heptaginę prizmę, tokią kaip: jos konstrukcija, jos pagrindų savybės, visų jos veidų plotas ir tūris.
1 - Statyba
Konstrukcijai heptaginę prizmę reikia dviejų, o tai bus jos pagrindai ir septyni lygiagretės, po vieną kiekvienoje heptagono pusėje..
Pradėkite braižydami heptagoną, tada nubrėžkite septynias vertikalias, vienodo ilgio linijas, kurios yra iš kiekvienos jos viršūnės.
Galiausiai sudaromas dar vienas heptagonas, kad jo viršūnės sutaptų su ankstesniame etape sudarytų linijų galu.
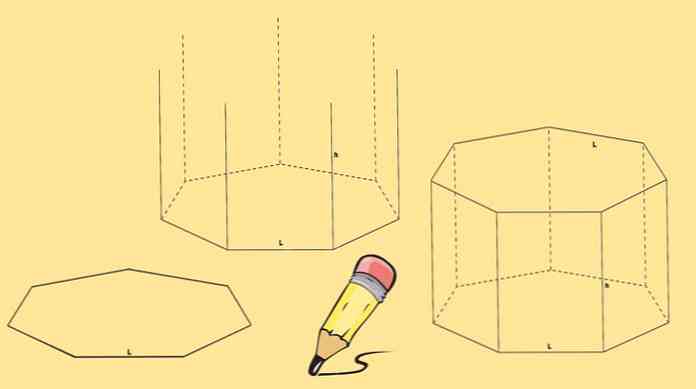
Viršutinė heptaginė prizmė vadinama tiesia heptagonine prizmu. Bet jūs taip pat galite turėti įstrižą heptagoninę prizmę, panašią į žemiau pateiktą paveikslą.

2- Jo pagrindų savybės
Kadangi jų pagrindai yra heptagonai, jie atitinka tai, kad įstrižainės skaičius yra D = nx (n-3) / 2, kur „n“ yra daugiakampio šonų skaičius; šiuo atveju mes turime, kad D = 7 × 4/2 = 14.
Taip pat matome, kad bet kurio heptagono (reguliaraus ar nereguliaraus) vidinių kampų suma yra lygi 900º. Tai galima patvirtinti šiuo paveikslėliu.
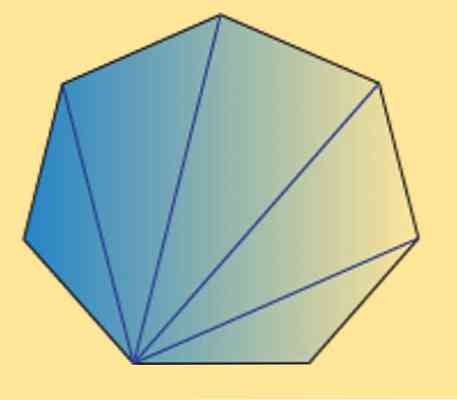
Kaip matote, yra 5 vidiniai trikampiai ir, naudojant trikampio vidinių kampų sumą, lygus 180º, galima gauti, kad norimas rezultatas.
3 - Plotas, reikalingas Heptagoniniam prizmui sukurti
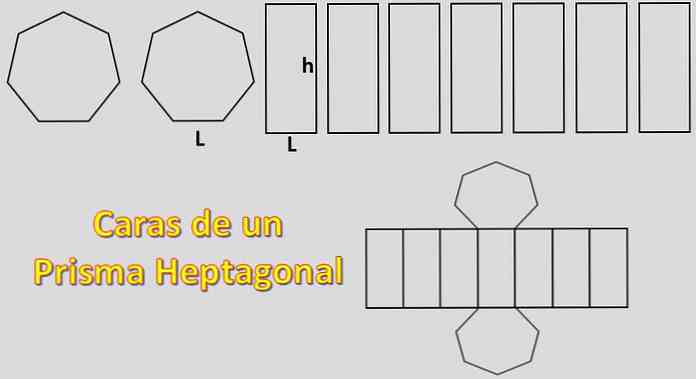
Kadangi jos pagrindai yra du heptagonai, o jų šoninės yra septynios lygiagretės, sritis, reikalinga heptaginės prizmės konstravimui, yra lygi 2xH + 7xP, kur „H“ yra kiekvieno heptagono plotas ir „P“ kiekvienos lygiagretės plotis.
Tokiu atveju bus apskaičiuojamas reguliaraus heptagono plotas. Dėl to svarbu žinoti apothema apibrėžimą.
Apothem yra statmena linija, kuri eina nuo reguliaraus daugiakampio centro iki bet kurios jo pusės vidurio.
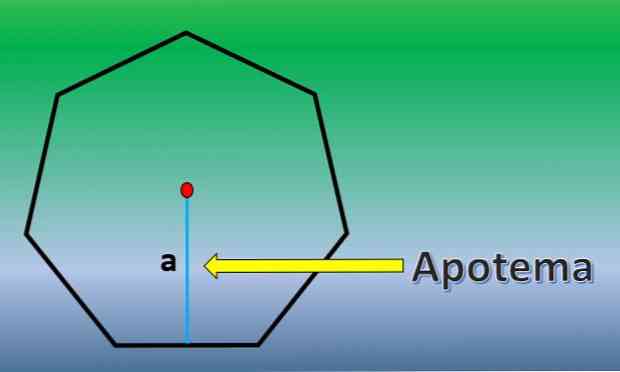
Kai žinomas apothem, heptagono plotas yra H = 7xLxa / 2, kur „L“ yra kiekvienos pusės ilgis ir „a“ apothem ilgis..
Lygiagretės plotą lengva apskaičiuoti, jis apibrėžiamas kaip P = Lxh, kur „L“ yra vienodo ilgio heptagono ir „h“ ilgio prizmės aukštis.
Apibendrinant galima pasakyti, kad medžiagos, reikalingos heptagoninei prizmei (reguliarioms bazėms), kiekis yra 7xLxa + 7xLxh, ty 7xL (a + h).
4- Tomas
Kai žinoma pagrindo ir prizmės aukštis, tūris apibrėžiamas kaip (bazinis plotas) x (aukštis).
Heptaginės prizmės (su reguliariu pagrindu) atveju jo tūris yra V = 7xLxaxh / 2; taip pat gali būti parašyta kaip V = Pxaxh / 2, kur „P“ yra įprastinio heptagono perimetras.
Nuorodos
- Billstein, R., Libeskind, S., ir Lott, J. W. (2013). Matematika: problemos sprendimo būdas pagrindinio ugdymo mokytojams. López Mateos redaktoriai.
- Fregoso, R. S., ir Carrera, S. A. (2005). Matematika 3. Redakcija Progreso.
- Gallardo, G., ir Pilar, P. M. (2005). Matematika 6. Redakcija Progreso.
- Gutiérrez, C. T., ir Cisneros, M. P. (2005). 3-asis matematikos kursas. Redakcija Progreso.
- Kinsey, L., ir Moore, T. E. (2006). Simetrija, forma ir erdvė: matematikos įvedimas per geometriją (iliustruotas, atspausdintas). „Springer Science & Business Media“.
- Mitchell, C. (1999). Apibūdinantys „Math Line“ dizainai (Illustrated ed.). Scholastic Inc.
- R., M. P. (2005). Aš piešiu 6º. Redakcija Progreso.


