Kapiliarinės savybės ir pavyzdys vandenyje
The kapiliarumas Tai yra skysčių savybė, leidžianti jiems judėti per vamzdines skyles ar akytas paviršius netgi nuo sunkio jėgos. Tam reikia turėti dvi jėgas, susijusias su skystomis molekulėmis: sanglaudą ir sukibimą; turintys šiuos du fizinius atspindžius, vadinamus paviršiaus įtempimu.
Skystis turi sugebėti sudrėkinti vidines vamzdelio sienas arba medžiagos, per kurią jis juda, poras. Taip atsitinka, kai sukibimo jėga (kapiliarinio vamzdžio skysčio siena) yra didesnė už tarpmolekulinę sanglaudos jėgą. Todėl skystosios molekulės sukuria stipresnę sąveiką su medžiagos atomais (stiklu, popieriumi ir tt) nei tarp jų.
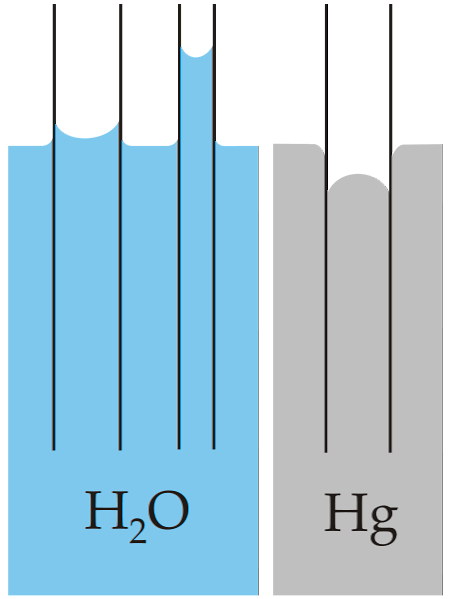
Klasikinis kapiliarumo pavyzdys parodytas palyginus šią savybę dviem labai skirtingais skysčiais: vandeniu ir gyvsidabriu.
Viršutinis vaizdas rodo, kad vanduo kyla per vamzdžio sieneles, o tai reiškia, kad jis turi didesnes sukibimo jėgas; priešingai nei gyvsidabriui, nes jos darnios, metalinės rišamosios jėgos neleidžia jam sudrėkinti stiklo.
Dėl šios priežasties vanduo sudaro įgaubtą menizmą, o gyvsidabris - išgaubtas meniskus (kupolo formos). Taip pat reikėtų pažymėti, kad kuo mažesnis vamzdžio spindulys arba sekcija, per kurią skystis juda, tuo didesnis aukštis arba nuvažiuotas atstumas (palyginkite abiejų vamzdžių vandens stulpelių aukštį).
Indeksas
- 1 Kapiliarumo ypatybės
- 1.1 - Skysčio paviršius
- 1.2. Aukštis
- 1.3. Paviršiaus įtampa
- 1.4. Kapiliarų arba porų, kuriuose skystis pakyla, rodmuo
- 1,5 - kontakto kampas (θ)
- 2 Vandens kapiliarumas
- 2.1 Augaluose
- 3 Nuorodos
Kapiliarumo ypatybės
-Skysčio paviršius
Skysčio paviršius, ty vandens, kapiliaruose yra įgaubtas; ty meniskas yra įgaubtas. Tokia situacija kyla dėl to, kad jėgos, veikiančios vandens molekules, esančios šalia vamzdžio sienelės, yra nukreiptos į tai.
Visame menyje yra kontaktinis kampas (θ), kuris yra kampas, kuris suformuoja kapiliarinio vamzdžio sienelę su linijos liestine ant skysčio paviršiaus kontakto vietoje..
Sukibimo ir sanglaudos jėgos
Jei skysčio sukibimo jėga į kapiliarinę sienelę viršija tarpmolekulinę sanglaudos jėgą, tada kampas yra θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
Kai ant švaraus stiklo paviršiaus dedamas vandens lašas, ant stiklo plinta vanduo, kad θ = 0 ir cos θ = 1.
Jei tarpmolekulinė sanglaudos jėga vyrauja virš kapiliarinio skysčio sienelės sukibimo stiprumo, pvz., Gyvsidabrio, menisks bus išgaubtas, o kampas θ bus> 90º; gyvsidabris nedažo kapiliarinės sienos ir todėl nusileidžia per vidinę sieną.
Kai ant švaraus stiklo paviršiaus dedamas lašas gyvsidabrio, lašas išlaiko savo formą ir kampas θ = 140º.
-Aukštis
Per kapiliarinį vamzdelį vanduo pakyla iki aukščio (h), kuriame vandens kolonėlės svoris kompensuoja vertikalią tarpmolekulinės sanglaudos jėgos dalį.
Kadangi daugiau vandens pakyla, ateis taškas, kuriame gravitacija sustabdys jo kilimą, net jei paviršiaus įtampa veikia jūsų naudai.
Kai taip atsitinka, molekulės negali toliau „lipti“ į vidines sienas, o visos fizinės jėgos yra lyginamos. Viena vertus, jūs turite jėgų, skatinančių vandens kilimą, ir, kita vertus, savo svorį.
Jurino įstatymas
Tai galima parašyti matematiškai taip:
2 π rΥcosθ = ρgπr2h
Kai kairiosios lygties pusė priklauso nuo paviršiaus įtampos, kurios dydis taip pat yra susijęs su sanglaudos ar tarpmolekulinėmis jėgomis; Cosθ reiškia kontaktinį kampą ir r skylės spindulį, per kurį skystis pakyla.
Ir dešinėje lygties pusėje mes turime aukštį h, sunkio jėgą g ir skysčio tankį; tai būtų vanduo.
Tuomet jūs turite kliringo
h = (2Υcosθ / ρgr)
Ši formuluotė yra žinoma kaip Jurino įstatymas, kuris apibrėžia skysčio kolonėlės aukštį, pasiektą kapiliariniame vamzdelyje, kai skysčio kolonėlės svoris yra subalansuotas su kapiliarinės pakilimo jėga.
-Paviršiaus įtampa
Vanduo yra dipolinė molekulė dėl deguonies atomo ir molekulinės geometrijos elektronegatyvumo. Dėl to vandens molekulės dalis, kurioje yra deguonis, yra neigiamai įkrauta, o vandens molekulės dalis, turinti 2 vandenilio atomus, yra teigiamai įkrauta..
Dėl to skysčio molekulės sąveikauja dėl daugelio vandenilio jungčių, išlaikydamos jas kartu. Tačiau vandens molekulės, kurios yra sąsajos vandenyje: ore (paviršiuje), yra skysčio sinuso molekulių neto pritraukimo, nekompensuojamos su silpnu oro molekulių patrauklumu..
Todėl sąsajos vandens molekulės yra patrauklios jėgos, kurios linkusios pašalinti sąsajos vandens molekules; tai yra, vandenilio tiltai, suformuoti su dugne esančiomis molekulėmis, kurios yra ant paviršiaus. Taigi, paviršiaus įtempis siekia sumažinti vandens paviršių: oro sąsają.
Ryšys su h
Jei pažvelgsite į Jurino įstatymo lygtį, pamatysite, kad h yra tiesiogiai proporcingas Υ; todėl kuo didesnė skysčio paviršiaus įtampa, tuo didesnis aukštis, kuris gali pakilti per medžiagos kapiliarą arba poras.
Taigi galima tikėtis, kad dviejų skysčių, A ir B, kurių paviršiaus įtempiai yra skirtingi, didžiausias paviršiaus įtempimas padidėja iki aukštesnio aukščio.
Iš to galima daryti išvadą, kad didelė paviršiaus įtampa yra svarbiausia savybė, kuri apibrėžia skysčio kapiliarinę savybę.
-Kapiliarų spindulys arba poros, kur skystis pakyla
Jurino įstatymo stebėjimas rodo, kad skysčio kapiliaruose arba porose pasiekiamas aukštis yra atvirkščiai proporcingas to paties spinduliui..
Todėl kuo mažesnis spindulys, tuo didesnis aukštis, kurį skysčio kolonėlė pasieks kapiliarinį poveikį. Tai galima matyti tiesiogiai vaizde, kuriame vanduo lyginamas su gyvsidabriu.
Stiklo mėgintuvėlyje, kurio spindulys yra 0,05 mm, vandens kolonėlė pagal kapiliarumą pasieks 30 cm aukštį. Kapiliariniuose vamzdeliuose, kurių spindulys yra 1 μm ir kurio siurbimo slėgis yra 1,5 x 103 hPa (kuri yra lygi 1,5 atm) atitinka vandens stulpelio aukščio apskaičiavimą nuo 14 iki 15 m.
Tai labai panaši į tai, kas vyksta su šia šiaudais, kurios savaime sukasi keletą kartų. Imant skystį, susidaro slėgio skirtumas, dėl kurio skystis pakyla į burną.
Didžiausia stulpelio aukščio vertė, pasiekta kapiliarumu, yra teorinė, nes kapiliarų spindulys negali būti mažesnis už tam tikrą ribą.
Poiseuilio įstatymas
Tai patvirtina, kad tikrojo skysčio srautas gaunamas pagal šią formuluotę:
Q = (πr4/ 8ηl) ΔP
Kai Q yra skysčio srautas, η yra jo klampumas, l vamzdžio ilgis ir ΔP slėgio skirtumas.
Mažinant kapiliarų spindulį, skysčio kolonėlės aukštis, pasiektas kapiliarumu, turėtų išaugti neribotą laiką. Tačiau Poiseuille nurodo, kad spindulio mažinimas taip pat sumažina skysčio srautą per tą kapiliarą.
Be to, klampumas, kuris yra atsparumo, kuris prieštarauja tikro skysčio srautui, matas, dar labiau sumažintų skysčio srautą..
-Kontaktinis kampas (θ)
Kuo didesnė cosθ vertė, tuo didesnis vandens kolonėlės aukštis pagal kapiliarumą, kaip nurodyta Jurino įstatyme.
Jei θ yra mažas ir artėja prie nulio (0), cosθ yra = 1, todėl reikšmė h bus maksimali. Priešingai, jei θ yra lygus 90º, cosθ = 0 ir h = 0 vertė.
Kai θ vertė yra didesnė nei 90º, o tai yra išgaubto meniškio atvejis, skystis nepadidėja kapiliarumu, o jo tendencija nusileisti (kaip gyvsidabris)..
Vandens kapiliarumas
Vandens paviršiaus įtempimo vertė yra 72,75 N / m, palyginti didelė, palyginti su šių skysčių paviršiaus įtempių vertėmis:
-Acetonas: 22,75 N / m
-Etilo alkoholis: 22,75 N / m
-Heksanas: 18,43 N / m
-Metanolis: 22,61 N / m.
Todėl vanduo turi išskirtinę paviršiaus įtampą, kuri skatina kapiliarinio reiškinio, reikalingo vandens ir maistinių medžiagų įsisavinimui, plėtrą..
Ant augalų

Kapiliarumas yra svarbus mechanizmas, padedantis augalams auginti sultis, bet nepakanka, kad sultys pasiektų medžių lapus..
Perpylimas arba garavimas yra svarbus mechanizmas, kai augalų ksilemas padidėja. Lapai praranda vandenį išgarinant, todėl sumažėja vandens molekulių kiekis, dėl kurio traukiasi kapiliariniuose vamzdeliuose esančios vandens molekulės (xylem).
Vandens molekulės neveikia nepriklausomai vienas nuo kito, bet sąveikauja su Van der Waals jėgomis, dėl kurių jie pakyla augalų kapiliarinių vamzdžių link lapų..
Be šių mechanizmų, reikėtų pažymėti, kad augalai absorbuoja vandenį iš dirvožemio osmoso būdu ir kad teigiamas slėgis, susidarantis šaknyje, skatina vandens kilimo pradžią per augalo kapiliarus.
Nuorodos
- García Franco A. (2010). Paviršiniai reiškiniai. Gauta iš: sc.ehu.es
- Paviršiaus reiškiniai: paviršiaus įtempis ir kapiliarumas. [PDF] Gauta iš: ugr.es
- Vikipedija. (2018). Kapiliarumas Gauta iš: en.wikipedia.org
- Risvhan T. (s.f.) Kapiliarumas augaluose. Gauta iš: academia.edu
- Helmenstine, Anne Marie, Ph.D. (2018 m. Gruodžio 22 d.). Kapiliarinis veiksmas: apibrėžimas ir pavyzdžiai. Gauta iš: thinkco.com
- Ellen Ellis M. (2018). Vandens kapiliarinis veiksmas: apibrėžimas ir pavyzdžiai. Tyrimas. Gauta iš: study.com
- „ScienceStruck“ personalas. (2017 m. Liepos 16 d.). Pavyzdžiai, paaiškinantys kapiliarinės veiklos koncepciją ir reikšmę. Gauta iš: sciencestruck.com


