Kiek kraštų yra šešiakampė prizmė?

Žinoti kiek kraštų yra šešiakampė prizmė „krašto“, „prizmės“ ir „šešiakampio“ reikšmė turi būti žinoma. Pirmosios dvi sąvokos yra bendrosios apibrėžtys, o trečioji sąvoka susijusi su geometrinio figūros forma.

Kalbant apie šešiakampį, paminėta šešiakampė (daugiakampis). Priedas „hexa“ rodo, kad daugiakampis turi šešias puses.

Kraštas yra objekto kraštas. Geometriniu požiūriu tai linija, jungianti dvi nuosekliąsias geometrinio figūros viršūnes.

Prizma yra geometrinis paveikslas, kurį riboja dvi lygiagrečios ir lygios daugiakampės bazės, o jų šoniniai veidai yra lygiagretės.

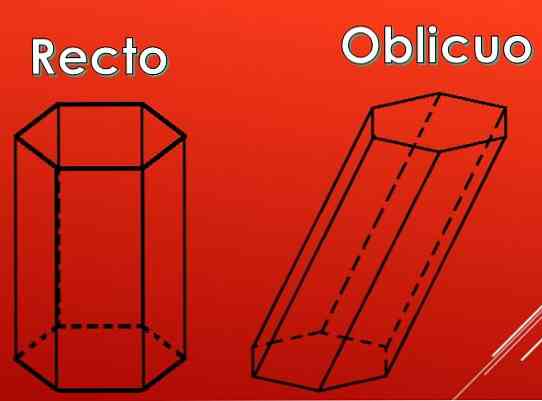
Tolesniame paveiksle matyti, kad šešiakampės prizmės šoniniai paviršiai gali būti stačiakampiai, tačiau jie taip pat gali būti lygiagretės.

Pagal paralelogramų tipą priemokos gali būti skirstomos į dvi rūšis: tiesias ir įstrižas.

Kaip skaičiuoti šešiakampės prizmės kraštus?

Briaunų, kurias turės šešiakampė prizmė, skaičius nepasikeis, jei tai yra tiesi arba įstrižinė prizmė. Be to, kraštų skaičius taip pat nepriklauso nuo šonų ilgio.

Skaitant šešiakampės prizmės kraštus galima atlikti keliais būdais. Štai du būdai:

1- Skilkite prizmę

Vienas iš būdų apskaičiuoti kraštus yra išskaidyti šešiakampę prizmę dviejose bazėse ir šonuose. Tokiu būdu jūs gaunate du šešiakampius ir lygiagretę su penkiomis vidinėmis linijomis.

Kiekvienas šešiakampis turi šešis kraštus, todėl prizme bus daugiau nei 12 briaunų.

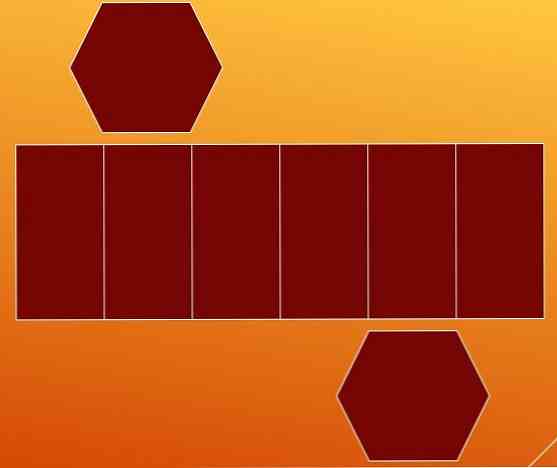
Iš pirmo žvilgsnio manoma, kad lygiagrečioje programoje yra devyni kraštai (septyni vertikalūs ir du horizontalūs). Tačiau patogu sustabdyti šio atvejo analizę.

Kai lygiagretė yra sulenkta, kad būtų suformuota prizmė, matyti, kad pirmoji eilutė kairėje bus su paskutine dešinėje esančia eilute, su kuria abi linijos atstovauja vieną kraštą.

Bet kaip apie dvi horizontalias linijas?

Kai visi gabalai vėl sujungti, horizontalios linijos bus sujungtos, kiekviena iš jų, su šešiais kiekvieno šešiakampio kraštais. Dėl šios priežasties jų skaičiavimas būtų klaidingas.

Taigi lygiagretės programoje yra šeši prizmės kraštai, kurie kartu su 12 briaunų, skaičiuojamų pradžioje, suteikia iš viso 18 briaunų.

2.- Kiekvieno krašto projektavimas

Kitas būdas - daug paprastesnis kraštų skaičiavimas - yra tai, kad šešiakampių prizmių pagrindai yra šešiakampiai, tada kiekviena bazė turi šešis kraštus.

Kita vertus, iš kiekvieno šešiakampio viršūnės yra nukreipiamas vienas kraštas į atitinkamą kito šešiakampio viršūnę; tai yra, yra šešios briaunos, kurios sujungia vieną bazę su kita.

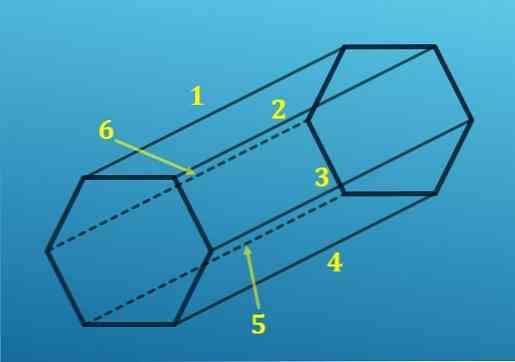
Pridėjus visus kraštus, gausite 18 briaunų.

Išvada

Galima įrodyti, kad prizmės briaunų skaičius yra lygus trims kartus didesniam kraštinių skaičiui, kurį sudaro daugiakampis jo formos.

Todėl penkiakampė prizmė turės 3 * 5 = 15 briaunų, heptaginė prizmė turės 3 * 7 = 21 briauną, todėl ji gali būti pritaikyta bet kuriam prizmui.

Nuorodos

1. Billstein, R., Libeskind, S., ir Lott, J. W. (2013). Matematika: problemos sprendimo būdas pagrindinio ugdymo mokytojams. López Mateos redaktoriai.
2. Fregoso, R. S., ir Carrera, S. A. (2005). Matematika 3. Redakcija Progreso.
3. Gallardo, G., ir Pilar, P. M. (2005). Matematika 6. Redakcija Progreso.
4. Gutiérrez, C. T., ir Cisneros, M. P. (2005). 3-asis matematikos kursas. Redakcija Progreso.
5. Kinsey, L., ir Moore, T. E. (2006). Simetrija, forma ir erdvė: matematikos įvedimas per geometriją (iliustruotas, atspausdintas). „Springer Science & Business Media“.
6. Mitchell, C. (1999). Apibūdinantys „Math Line“ dizainai (Illustrated ed.). Scholastic Inc.
7. R., M. P. (2005). Aš piešiu 6º. Redakcija Progreso.