Archimedas Biografija, įnašai ir išradimai
Siribusa Archimedas (287 a.C - 212 a.C) buvo matematikas, fizikas, išradėjas, inžinierius ir graikų astronomas iš senovės Sirakūzų miesto Sicilijos saloje. Jo didžiausias įnašas yra Archimedo principas, išgyvenimo metodo kūrimas, mechaninis metodas arba pirmojo planetariumo sukūrimas..
Šiuo metu ji laikoma viena iš trijų svarbesnių senovės matematikos figūrų, esančių šalia Euclides ir Apolonio, nes jos indėlis buvo svarbus mokslo pasiekimas skaičiavimo, fizikos, geometrijos ir astronomijos srityse. Savo ruožtu, tai daro jį vienu ryškiausių mokslininkų žmonijos istorijoje.

Nors yra mažai informacijos apie jo asmeninį gyvenimą, ir žinomi yra abejotini patikimumo duomenys, tačiau jo įnašai žinomi dėka rašytinių laiškų apie savo kūrinius ir pasiekimus, kurie buvo išsaugoti iki dabarties, priklausantys į susirašinėjimą, kurį jis ilgus metus saugojo su draugais ir kitais to laiko matematikais.
Archimedas savo laiku garsėjo savo išradimais, kurie pritraukė savo amžininkų dėmesį, iš dalies dėl to, kad jie buvo naudojami kaip kariniai įrenginiai, siekiant sėkmingai išvengti daugelio romėnų invazijų..
Tačiau sakoma, kad jis teigė, jog vienintelis labai svarbus dalykas buvo matematika ir kad jo išradimai buvo tik taikytos geometrijos pramogos. Pogimdymuose jo darbai grynoje matematikoje buvo labiau vertinami nei jo išradimai.
Indeksas
- 1 Biografija
- 1.1 Mokymas
- 1.2 Mokslinis darbas
- 1.3 Konfliktas Sirakūzuose
- 1.4 Mirtis
- 2 Archimedo mokslinis indėlis
- 2.1 Archimedo principas
- 2.2 Mechaninis metodas
- 2.3 Svirties teisės paaiškinimas
- 2.4 Mokslinių tyrimų demonstravimo metodo tobulinimas
- 2.5 Apskritimo matas
- 2.6 Sferų ir cilindrų geometrija
- 3 Išradimai
- 3.1 Odometras
- 3.2 Pirmasis planetariumas
- 3.3 Archimedo varžtas
- 3.4 Archimedo žnyplė
- 4 Nuorodos
Biografija
Siribuso archimedas gimė maždaug 287 m. Nėra daug informacijos apie jo ankstyvuosius metus, nors galima sakyti, kad jis gimė Sirakūzuose, miestas, laikomas pagrindiniu Sicilijos salos uostu, šiandien Italijoje..
Tuo metu Sirakūzai buvo vienas iš miestų, sudariusių vadinamąją Magna Greciją, kurioje gyveno graikų kilmės gyventojai į pietinę Italijos ir Sicilijos pusiasalio teritoriją..
Nėra jokių žinomų faktų apie Archimedo motiną. Kalbant apie tėvą, žinoma, kad tai buvo vadinama Fidija ir kad jis buvo skirtas astronomijai. Ši jo tėvo informacija yra žinoma dėl knygos fragmento Smėlio skaitiklis, parašė Archimedas, kuriame jis paminėjo savo tėvo vardą.
Heraklides, kuris buvo graikų filosofas ir astronomas, labai patiko Archimedui ir netgi parašė apie jį biografiją. Tačiau šis dokumentas nebuvo išsaugotas, todėl visa jame esanti informacija nežinoma.
Kita vertus, istorikas, filosofas ir biografas Plutarco savo knygoje „Paraleliniai gyvenimai“ nurodė, kad Archimedas turėjo kraujo ryšį su Hiero II, tyrantu, kuris buvo atsakingas Sirakūzuose nuo 265 m..
Mokymas
Dėl mažos informacijos, kurią mes turime apie Archimedą, mes nežinome, kur jis gavo pirmąjį mokymą.
Tačiau įvairūs istoriografai nustatė, kad yra didelė tikimybė, kad Archimedas studijavo Aleksandrijoje, kuri buvo svarbiausias Graikijos kultūros ir mokymo centras regione..
Ši prielaida paremta Graikijos istoriko Diodoro Sículo pateikta informacija, kuri nurodė, kad Archimedas tikriausiai studijavo Aleksandrijoje.
Be to, daugelyje jo darbų pats Archimedas paminėjo kitus to laiko mokslininkus, kurių darbas buvo sutelktas Aleksandrijoje, todėl galima daryti prielaidą, kad jis iš tiesų sukūrė tą miestą.
Kai kurios asmenybės, su kuriomis manoma, kad Aleksandrijoje bendrauja Archimedas, yra geografas, matematikas ir astronomas Eratostenas iš Cyrene, matematikas ir astronomas Conon de Sanos.
Šeimos motyvacija
Kita vertus, tai, kad Archimedo tėvas buvo astronomas, galėjo turėti didelę įtaką vėlesniems jo pasirodymams, nes vėliau ir nuo senatvės buvo ypatingas patrauklumas. mokslai.
Po jo laiko Aleksandrijoje, manoma, kad Archimedas sugrįžo į Sirakūzus.
Mokslinis darbas
Grįžęs į Sirakūzus, Archimedas pradėjo kurti įvairius artefaktus, kurie greitai laimėjo jam tam tikrą populiarumą tarp šio miesto gyventojų. Per šį laikotarpį jis visiškai pasidavė moksliniam darbui, sukūrė įvairius išradimus ir padarė keletą matematinių sampratų, kurios buvo labai pažengusios į savo laiką.
Pavyzdžiui, kai jis atsidavė kietųjų kreivų ir plokščių figūrų charakteristikų tyrimui, jis sukūrė koncepcijas, susijusias su integriniu ir diferenciniu skaičiavimu, kuris buvo sukurtas vėliau.
Be to, Archimedas buvo tas, kuris nustatė, kad su sfera susijęs tūris atitinka dvigubą baliono, kuriame jis yra, dydį ir buvo tas, kuris išrado kompozicinį skriemulį, remdamasis jo atradimais apie svirties teisę..
Konfliktas Sirakūzuose
213 m. Pr. Kr. Romos kareiviai įžengė į Sirakūzų miestą ir apsupo savo gyventojus, kad juos perduotų.
Šį veiksmą vadovavo karinis ir graikų politikas Marco Claudio Marcelo pagal Antrąjį Punų karą. Vėliau jis buvo žinomas kaip Romos kardas, nes jis nugalėjo Sirakūzus.
Dvejus metus trukusio konflikto viduryje Sirakūzų gyventojai drąsiai ir žiauriai kovojo prieš romėnus, o Archimedas atliko labai svarbų vaidmenį, nes jis įsipareigojo kurti įrankius ir priemones, kurios padėjo nugalėti romėnus.
Galiausiai Marco Claudio Marcelo paėmė Sirakūzų miestą. Prieš didįjį Archimedo intelektualumą, Marcelo įsakė, kad jie nebūtų sužeisti ar nužudyti. Tačiau Archimedas buvo nužudytas Romos kareivio rankose.
Mirtis
Archimedas mirė 212 m. Praėjus daugiau nei 130 metų po mirties, 137-ią metų pr. Kr. Rašytojas, politikas ir filosofas Marco Tulio Cicero užėmė Romos administracijos pareigas ir norėjo rasti Archimedo kapą.
Ši užduotis nebuvo lengva, nes „Cicero“ niekas negalėjo rasti tikslios vietos. Tačiau jis galiausiai jį gavo, labai arti Agrigento durų ir apgailėtinomis sąlygomis.
Cicero išvalė kapą ir sužinojo, kad jis buvo užrašytas balionu esančiu rutuliu, kaip nuoroda į tai, kad Archimedesas padarė šiek tiek laiko..
Jo mirties versijos
Pirmoji versija
Viena iš versijų nurodo, kad Archimedas buvo sprendęs matematinę problemą, kai jam kreipėsi Romos kareivis. Sakoma, kad Archimedas galėjo jam tam tikrą laiką paprašyti išspręsti šią problemą, todėl kareivis jį būtų nužudęs.
Antroji versija
Antroji versija yra panaši į pirmąją. Atsižvelgiant į tai, kad Archimedas išsprendė matematikos problemą, kai įvyko miestas.
Romėnų kareivis įėjo į savo junginį ir įsakė jam susitikti su Marcelo, o Archimedas atsakė, kad jis turėjo išspręsti problemą, su kuria jis dirbo. Kareivis pasibjaurė dėl šio atsakymo ir jį nužudė.
Trečioji versija
Ši hipotezė rodo, kad Archimedas turėjo didelę matematikai būdingų priemonių įvairovę. Tada kareivis jį pamatė ir manė, kad jis gali turėti vertingų daiktų, todėl jis jį nužudė.
Ketvirtoji versija
Ši versija iliustruoja, kad Archimedas buvo prikabintas prie žemės, svarstydamas planus, kuriuos jis studijavo. Matyt, romėnų kareivis atėjo iš užpakalinės, ir nežinojo, kad tai buvo Archimedas.
Archimedo moksliniai įnašai
Archimedo principas
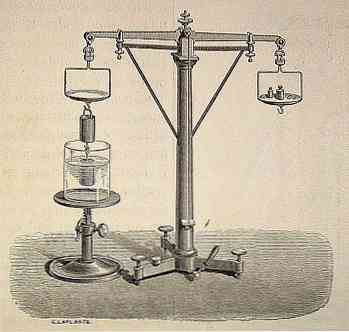
Archimedo principą šiuolaikinis mokslas laiko vienu iš svarbiausių senovės laikų palikimų.
Per visą istoriją, ir žodžiu, buvo pranešta, kad Archimedas atsitiko atsitiktinai padėkodamas karaliui Hieronui, kad jis pamatytų, ar aukso karūna, siunčiama gaminti jam, buvo padaryta tik auksu grynas ir neturėjo jokio kito metalo. Aš turėjau tai atlikti nepažeisdamas vainiko.
Sakoma, kad tuo metu, kai Archimedas meditavo, kaip išspręsti šią problemą, jis nusprendė maudytis, o kai jis įėjo į vonią, jis suprato, kad vanduo padidėjo lygiai, kai jis įsiliejo į jį..
Tokiu būdu jis atras mokslinį principą, kad „kiekvienas kūnas, visiškai ar iš dalies panardintas į skystį (skystį ar dujas), gauna didėjančią trauką, lygų skysčio svoriui, kuris yra išstumtas iš objekto“..
Šis principas reiškia, kad skysčiai patiria didėjančią jėgą, stumiantį į viršų, ant bet kokio joje įmerkto objekto, ir kad šios stumiamosios jėgos kiekis yra lygus panardinto kūno išstumto skysčio svoriui, nepriklausomai nuo jo svorio..
Šio principo paaiškinimas apibūdina flotacijos reiškinį, ir jis randamas jo Sutartis dėl plūduriuojančių kūnų.
Archimedo principas buvo gerokai taikomas palikuonims masinio naudojimo objektų, pavyzdžiui, povandeninių laivų, laivų, gelbėtojų ir balionų, plaukimui.
Mechaninis metodas
Kitas svarbiausias Archimedo indėlis į mokslą buvo grynai mechaninio, tai yra techninio metodo, įtraukimas į geometrinių problemų argumentavimą ir argumentavimą, o tai reiškė precedento neturintį būdą išspręsti šio tipo problemas tuo metu..
Archimedo kontekste geometrija buvo laikoma tik teoriniu mokslu, o bendras dalykas buvo tas, kad gryna matematika nusileido į kitus praktinius mokslus, kuriuose galėtų būti taikomi jos principai..
Dėl šios priežasties šiandien ji laikoma mechanikos, kaip mokslo disciplinos, pirmtake.
Rašte, kuriame matematikas atskleidžia naująjį metodą savo draugui Eratosthenes, nurodoma, kad tai leidžia spręsti matematikos klausimus per mechaniką ir kad šiek tiek lengviau sukurti geometrinės teoremos demonstravimą, jei tai jau yra turėti tam tikrų išankstinių praktinių žinių, kad jei neturite jokios idėjos apie tai.
Šis naujas Archimedo atliktas tyrimo metodas taptų neformalaus šiuolaikinio mokslinio metodo atradimo ir hipotezės formulavimo pirmtaku..
Svirties teisės paaiškinimas
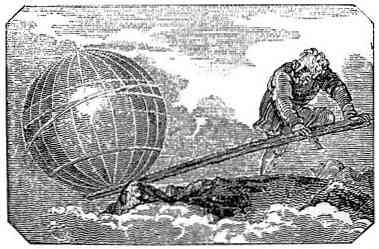
Nors svirtis yra paprasta mašina, kuri buvo naudojama nuo daug anksčiau nei Archimedas, jis sukūrė principą, paaiškinantį jo veikimą jo lėktuve..
Formuluodamas šį įstatymą, Archimedas nustato principus, apibūdinančius skirtingą svirties elgesį, kai ant jo dedami du kūnai, priklausomai nuo jo svorio ir atstumo nuo atramos taško.
Tokiu būdu jis nurodo, kad du kūnai, kuriuos galima išmatuoti (proporcingai), esantys ant svirties, yra subalansuoti, kai jie yra atstumu, kuris yra atvirkščiai proporcingas jų svoriui..
Tuo pačiu būdu, neišmatuojami kūnai (kurių negalima išmatuoti) tai daro, tačiau šį įstatymą Archimedas galėjo įrodyti tik su pirmos rūšies kūnais..
Svirties principo formulavimas yra geras mechaninio metodo taikymo pavyzdys, nes, pasak jo, laiškas, nukreiptas į Dositeo, tai buvo atrasta per pirmąjį momentą taikant praktikoje įdiegtus mechanikos metodus..
Vėliau jis suformulavo juos taikant geometrijos metodus (teorinius). Iš šio eksperimento su kūnais taip pat buvo atskirta sunkio centro sąvoka.
Mokslinio demonstravimo pratęsimo ar išsekimo metodo kūrimas
Išnaudojimas - tai geometrijoje naudojamas metodas, kuris susideda iš geometrinių figūrų, kurių plotas yra žinomas užrašu ir apipavidalinimu, apytikslis kitame, kurio plotas yra žinomas..
Nors Archimedas nebuvo šio metodo kūrėjas, jis jį meistriškai sukūrė ir sugebėjo apskaičiuoti tikslą Pi vertę..
Archimedas, naudodamas išpurškimo metodą, užrašytas ir apribotas šešiakampis skersmuo 1, sumažindamas iki absurdo skirtumą tarp šešiakampių ir apskritimo ploto.
Norėdami tai padaryti, jis padalino šešiakampius, sukurdamas iki 16 pusių daugiakampius, kaip parodyta ankstesniame paveiksle.
Tokiu būdu jis nurodė, kad pi (santykio tarp apskritimo ilgio ir jo skersmens) vertė yra tarp reikšmių 3.14084507 ... ir 3.14285714 ... .
Archimedas meistriškai naudojo exhaución metodą, nes jis ne tik sugebėjo apytiksliai apskaičiuoti Pi vertę su klaidų riba, bet ir norėjo, bet ir todėl, kad Pi yra neracionalus skaičius, per šis metodas ir gauti rezultatai padėjo pamatus, kurie sudygtų begalinio skaičiavimo sistemoje, ir vėliau, šiuolaikiniame integruotame skaičiuotuve.
Apskritimo matas
Norėdami nustatyti apskritimo sritį, Archimedas naudojo metodą, kuris sudarė kvadratą, kuris tiksliai atitiko apskritimą.
Žinant, kad kvadrato plotas buvo jo pusių suma ir kad apskritimo plotas buvo didesnis, jis pradėjo dirbti, kad gautų apytikslius. Tai jis padarė pakeisdamas kvadratą 6-pusių daugiakampiais ir dirbdamas su sudėtingesniais daugiakampiais.
Archimedas buvo pirmasis matematikas istorijoje, norėdamas rimtai apskaičiuoti skaičių Pi.
Sferų ir cilindrų geometrija
Tarp devynių architektų darbą matematikos ir fizikos darbų sudarė du sferų ir cilindrų geometrijos tomai..
Šiame darbe nagrinėjama, ar bet kurios spindulio sferos paviršius yra keturis kartus didesnis už didžiausią jo ratą, o sferos tūris yra du trečdaliai baliono, kuriame jis yra užrašytas.
Išradimai
Odometras
Taip pat žinomas kaip kilometrai, tai buvo šio garsaus žmogaus išradimas.
Šis įrenginys buvo pastatytas pagal rato principą, kuris, pasukdamas, suaktyvina pavaras, leidžiančias apskaičiuoti nuvažiuotą atstumą..
Pagal tą patį principą, Archimedas sukūrė kelių tipų matuoklius kariniams ir civiliniams tikslams.
Pirmasis planetariumas
Remiantis daugelio klasikinių rašytojų, tokių kaip Cicero, Ovid, Claudian, Marciano Capela, Casiodoro, Sexto Empirico ir Lactantius, liudijimais, daugelis mokslininkų dabar priskiria Archimedui pirmojo pradinio planetariumo kūrimą.
Tai mechanizmas, kurį sudaro „sferų“ serija, kuri sugebėjo imituoti planetų judėjimą. Iki šiol šio mechanizmo detalės nežinomos.
Pasak Cicero, Archimedo pastatyti planetariumai buvo du. Vienoje iš jų buvo atstovaujama žemė ir įvairios jos artimosios žvaigždės.
Kitoje, su vienu sukimu, saulė, mėnulis ir planetos padarė savo nepriklausomus judesius, susijusius su fiksuotomis žvaigždėmis, tokiu pat būdu, kaip ir realią dieną. Pastarajame, be to, galima stebėti vienas po kito einančius mėnulio etapus ir užtemimus.
Archimedo varžtas
„Archimedes“ varžtas yra prietaisas, naudojamas vandeniui transportuoti iš apačios į viršų per šlaito, naudojant vamzdį arba cilindrą.
Pasak Graikijos istoriko Diodoro, šio išradimo dėka buvo palengvintas drėkinimas derlingose žemėse, esančiose prie Nilo upės senovės Egipte, nes tradicinės priemonės reikalavo didžiulės fizinės jėgos, išnaudojusios darbuotojus..
Naudojamas cilindras turi tą patį ilgį turintį varžtą, kuris palaiko tarpusavyje sujungtą sraigtų arba pelekų sistemą, kuri atlieka sukamąjį judėjimą, rankiniu būdu sukant sukamąja svirtimi.
Tokiu būdu sraigtai sugeba stumti bet kurią medžiagą iš apačios į viršų, formuodami tam tikrą begalinę grandinę.
Archimedo rankena
Archimedo žandikaulis arba geležies ranka, kaip ji taip pat žinoma, buvo vienas iš baisiausių karo ginklų, kurį sukūrė šis matematikas, tapęs svarbiausiu Sicilijos gynybos romėnų invazijos metu..
Remiantis Drexel universiteto profesorių Chris Rorres (Matematikos katedra) ir Harry Harris (Civilinės inžinerijos ir architektūros katedra) atliktais tyrimais, tai buvo didelė svirtis, turėjusi prie svirties pritvirtintą kabliuką grandinę, kuri pakabino nuo jos.
Per svirtį kablys buvo manipuliuojamas taip, kad nukrito ant priešo laivo, o tikslas buvo pakabinti jį ir pakelti jį tokiu mastu, kad jį išlaisvinant būtų galima visiškai nugriauti arba nukentėti ant kranto esančių uolų..
Rorresas ir Harris pristatė simpoziumą "Mašinos ir ypatingosios senovinės struktūros" (2001), miniatiūrinę šio artefakto reprezentaciją "Siaubingas karo mašina: Archimedo geležies rankų statyba ir eksploatavimas"
Šio darbo realizavimui jie rėmėsi senovės istorikų Polibio, Plutarco ir Tito Livio argumentais..
Nuorodos
- ASSIS, A. (2008). Archimedas, sunkio centras ir pirmasis mechanikos įstatymas [internete]. Prieiga prie birželio 10, 2017 apie bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedas [internete]. Pasiekta 2015 m. Birželio 9 d. World Wide Web: books.google.co.ve/books.
- MOLINA, A. (2008). Sirakūzų Archimedo tyrimo metodas: intuicija, mechanika ir išbandymas [internete]. Pasiekta 2017 m. Birželio 10 d., World Wide Webproduccioncientifica.luz.edu.
- O'CONNOR, J. & ROBERTSON, R. (1999). Sirijaus Archimedas [internete]. Prieiga prie 2017 m. Birželio 9 d. Adresu history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Archimedas: jo gyvenimas, darbai ir įmokos šiuolaikinei matematikai [internete]. Gauta 2017 m. Birželio 9 d., Adresu lfunes.uniandes.edu.co.
- QUINN, L. (2005). Sirijaus Archimedas [internete]. Prieiga prie 2017 m. Birželio 9 d. Adresu math.ucdenver.edu.
- RORRES, C. & HARRIS, H. (2001). Siaubingas karo mašina: Archimedo geležies rankų statyba ir eksploatavimas [internete]. Gauta 2017 m. Birželio 10 d. Adresu cs.drexel.edu.
- VITE, L. (2014). Archimedo principas [internete]. Gauta 2017 m. Birželio 10 d. Adresu repository.uaeh.edu.mx.


