Kolinijinė sistema ir pavyzdžiai

The kolinijiniai vektoriai Jie yra vienas iš trijų esamų vektorių tipų. Tai yra tie vektoriai, kurie yra toje pačioje kryptyje arba veikimo linijoje. Tai reiškia, kad du ar daugiau vektorių bus kolinariniai, jei jie yra išdėstyti tiesiomis linijomis, kurios yra lygiagrečios viena kitai.

Vektorius apibrėžiamas kaip kiekis, taikomas kūnui ir apibūdinamas kaip kryptis, prasmė ir skalė. Vektorius galima rasti plokštumoje arba erdvėje ir gali būti įvairių tipų: kolinijiniai vektoriai, lygiagretūs vektoriai ir lygiagretūs vektoriai.

Indeksas

• 1 kolinealiniai vektoriai
• 2 Charakteristikos
  • 2.1 1 pavyzdys
  • 2.2 2 pavyzdys
  • 2.3 1 pavyzdys
• 3 Kolinijinė vektorinė sistema
  • 3.1 Kolinijiniai vektoriai su priešingais jutimais
  • 3.2. Kolinijiniai vektoriai su ta pačia prasme
  • 3.3 Kolinijiniai vektoriai, turintys vienodą dydį ir priešingus pojūčius
• 4 Skirtumas tarp kolinijinių ir lygiagrečių vektorių
• 5 Nuorodos

Kolinijiniai vektoriai

Vektoriai yra kolinariniai, jei vienos linijos veikimo linija yra lygiai tokia pati visų kitų vektorių veikimo linija, nepriklausomai nuo kiekvieno vektoriaus dydžio ir prasmės.

Vektoriai naudojami kaip reprezentacijos įvairiose srityse, pavyzdžiui, matematikos, fizikos, algebros ir geometrijos srityse, kur vektoriai yra kolinijiniai tik tada, kai jų kryptis yra vienoda, nepriklausomai nuo to, ar jų reikšmė nėra.

Savybės

- Dvi ar daugiau vektorių yra lygiagrečios, jei santykis tarp koordinatų yra lygus.

1 pavyzdys

Mes turime vektorius m = m_x; m_y ir n = n_x; n_y. Jos yra bendro pobūdžio, jei:

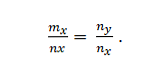
2 pavyzdys

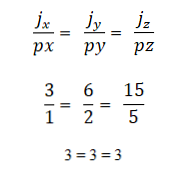
- Du ar daugiau vektorių yra kolinijiniai, jei produktas arba vektoriaus dauginimas yra lygus nuliui (0). Taip yra todėl, kad koordinačių sistemoje kiekvienas vektorius pasižymi atitinkamomis koordinatėmis, o jei jos yra proporcingos viena kitai, vektoriai bus kolinariniai. Tai išreiškiama taip:

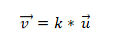
1 pavyzdys

Turime vektorius a = (10, 5) ir b = (6, 3). Siekiant nustatyti, ar jie yra kolinijiniai, taikoma determinantinė teorija, kuri nustato kryžminių produktų lygybę. Tokiu būdu jūs turite:

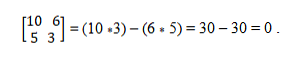
Colinear vektorinė sistema

Kolinijiniai vektoriai pateikiami grafiškai, naudojant šių krypčių kryptį ir prasmę, atsižvelgiant į tai, kad jie turi praeiti per taikomąją vietą ir modulį, kuris yra tam tikras skalė ar ilgis.

Kolinijinių vektorių sistema suformuojama, kai du ar daugiau vektorių veikia objektą ar kūną, atstovaujantys jėgą ir veikdami ta pačia kryptimi.

Pavyzdžiui, jei kūnui taikomos dvi kolinijinės jėgos, jų rezultatas priklausys tik nuo to, kokia kryptimi jie veikia. Yra trys atvejai:

Kolinijiniai vektoriai su priešingais jutimais

Dviejų kolinijinių vektorių rezultatas yra lygus šių sumų sumai:

R = Σ F = F₁ + F_2.

Pavyzdys

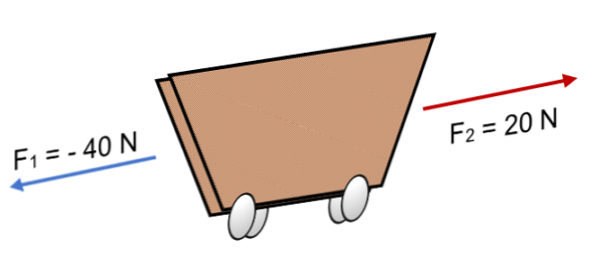
Jei dvi jėgos veikia krepšyje F₁ = 40 N ir F₂ = 20 N priešinga kryptimi (kaip parodyta paveikslėlyje), rezultatas yra:

R = Σ F = (- 40 N) + 20N.

R - - 20 N.

Kolinijiniai vektoriai su ta pačia prasme

Gautos jėgos dydis bus lygus kolinijinių vektorių sumai:

R = Σ F = F₁ + F_2.

Pavyzdys

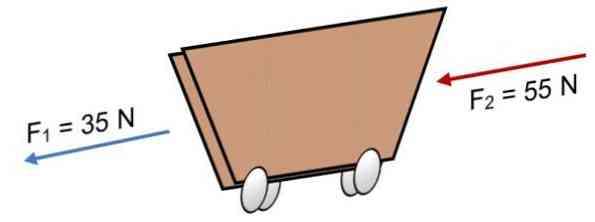
Jei dvi jėgos veikia krepšyje F₁ = 35 N ir F₂ = 55 N ta pačia kryptimi (kaip parodyta paveikslėlyje), rezultatas yra:

R = Σ F = 35 N + 55N.

R = 90 N.

Teigiamas rezultatas rodo, kad kolinijiniai vektoriai veikia į kairę.

Kolinijiniai vektoriai, turintys vienodą dydį ir priešingus pojūčius

Dviejų kolinijinių vektorių rezultatas bus lygus kolinijinių vektorių sumai:

R = Σ F = F₁ + F_2.

Kadangi jėgos turi tokį patį dydį, bet priešinga kryptimi, tai yra teigiamas, o kitas neigiamas - pridėjus dvi jėgas, rezultatas bus lygus nuliui.

Pavyzdys

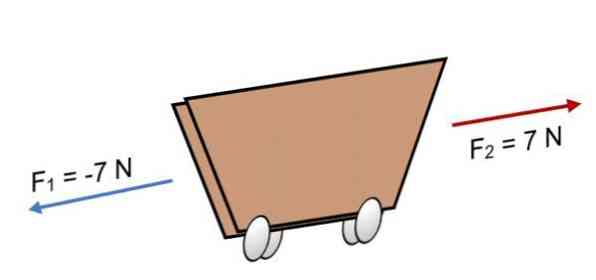
Jei dvi jėgos veikia krepšyje F₁ = -7 N ir F₂ = 7 N, kurių dydis yra toks pat, bet priešinga kryptimi (kaip parodyta paveikslėlyje), rezultatas yra:

R = ΣF = (-7 N) + 7N.

R = 0.

Kadangi rezultatas yra lygus 0, tai reiškia, kad vektoriai yra subalansuoti vienas su kitu ir todėl kūnas yra pusiausvyroje arba ramybėje (jis nesikeis).

Skirtumas tarp kolinijinių ir lygiagrečių vektorių

Kolinijiniai vektoriai pasižymi ta pačia kryptimi ta pačia kryptimi, arba todėl, kad jie yra lygiagrečiai linijai; tai yra, vektoriai yra tiesioginės lygiagrečios linijos.

Kita vertus, lygiagretūs vektoriai yra apibrėžti, nes jie yra skirtingose ​​veiklos srityse, kurios yra sulaikytos viename taške.

Kitaip tariant, jie turi tą patį kilmės ar atvykimo tašką, nepriklausomai nuo jų modulio, krypties ar krypties - tarp jų yra kampas.

Lygiagrečių vektorių sistemos sprendžiamos matematiniais metodais arba grafikais, kurie yra jėgų lygiagretės metodas ir jėgų poligono metodas. Per šiuos veiksnius bus nustatyta gauto vektoriaus vertė, nurodanti kūno judėjimo kryptį.

Iš esmės pagrindinis kolinijinių vektorių ir lygiagrečių vektorių skirtumas yra veiksmų linija, kurioje jie veikia: kolinijinės yra toje pačioje eilutėje, tuo tarpu tuo pačiu skirtingais..

Tai reiškia, kad kolinijiniai vektoriai veikia vienoje plokštumoje „X“ arba „Y“; ir tuo pačiu veiksmu abiejose plokštumose, pradedant tuo pačiu tašku.

Kolinijiniai vektoriai nėra taške, kaip ir tuo pačiu metu, nes jie yra lygiagrečiai vienas kitam.

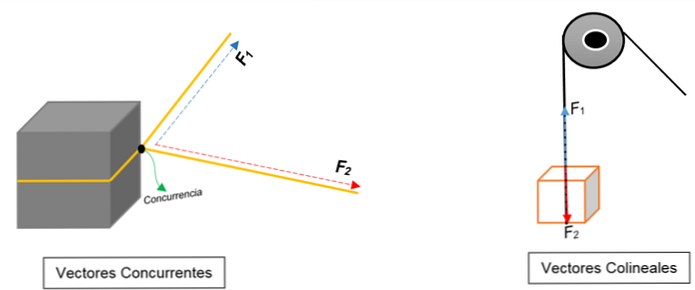
Kairiajame paveikslėlyje matote bloką. Ji yra susieta su virvele, o mazgas padalija į dvi dalis; kai traukiama link skirtingų krypčių ir skirtingų jėgų, blokas judės link tos pačios krypties.

Pateikiami du vektoriai, kurie sutampa su tašku (bloku), nepriklausomai nuo jų modulio, prasmės ar krypties.

Vietoj to, dešiniajame vaizde atsiranda skriemulys, kuris pakelia langelį. Virvė yra veiksmų linija; kai jis traukiamas, joje veikia dvi jėgos (vektoriai): viena įtempimo jėga (kai laipioti blokas) ir kita jėga, kuri daro bloko svorį. Abu turi tą pačią kryptį, bet priešinga kryptimi; nesutinkate.

Nuorodos

1. Estalella, J. J. (1988). Vektorių analizė. 1 tomas.
2. Gupta, A. (s.f.). Tata McGraw-Hill Švietimas.
3. Jin Ho Kwak, S. H. (2015). Linijinė algebra. „Springer Science & Business Media“.
4. Montiel, H. P. (2000). Fizika 1 technologiniam bakalaureatui. Patria redakcinė grupė.
5. Santiago Burbano de Ercilla, C. G. (2003). Bendra fizika Redakcinis Tebaras.
6. Sinha, K. (s.f.). Matematikos teksto knyga XII 2 tomas. Rastogi publikacijos.